Good Practice in der Elementanalyse – Teil III
Grundlagen der EDX wurden in Teil I, Spectrum 140, behandelt. Teil II (Spektrum 141) beschäftigte sich mit dem Einfluss von REM-Parametern auf die Analyseergebnisse. Der nun folgende Beitrag diskutiert einige Aspekte der quantitativen EDX.
Der Anspruch an eine quantitative EDX-Analyse („Verhältnis Element A zu Element B = x:y und damit Verbindung AnBm“) ist deutlich höher als an EDX-Analysen mit dem Ziel rein qualitativer Aussagen („Element X und Y in der Probe enthalten“). Für akkurate Quantifizierungen müssen bestimmte Parameter beachtet werden. Gründe dafür sind an unterschiedlichen Stellen zu suchen, letztlich sind es aber vor allem die von der EDX-Software verwendeten Algorithmen, welche eine Quantifizierung anhand idealisierter Modelle für die untersuchten Materialien durchführen und eine Kenntnis der Parameter erfordern. Die Probe sollte beispielsweise eine homogene Zusammensetzung und eine ebene Oberfläche besitzen, sowie der Arbeitsabstand den Herstellerangaben entsprechend eingestellt werden. Die Beschleunigungsspannung sollte mindestens das Anderthalbfache der Energie der zu untersuchenden Elementpeaks betragen. Zu hohe oder zu niedrige Strahlströme sind zu vermeiden (sinnvolle „Totzeit“). Eine Messung mit Standards erhöht die Sicherheit der Messergebnisse.
Vereinfacht betrachtet könnte man davon ausgehen, dass die Intensitäten der Peaks von Element A und Element B proportional zu deren Konzentration in der Probe sind. Der hohe Wirkungsquerschnitt von Röntgenstrahlung verkompliziert die Angelegenheit jedoch deutlich. Jedes Spektrum setzt sich aus Beiträgen durch Bremsstrahlung (Untergrund von EXRay = 0 bis EPE), Röntgenfluoreszenz und Eigenabsorption der Röntgenstrahlung zusammen. Hinzu kommen noch Peaküberlagerungen. Eine Peakentfaltung wird somit notwendig. In der einfachsten Version der Quantifizierung werden empirische Daten herangezogen, also eine Art Datenbank genutzt. Grundlegendes Modell für die quantitative EDX physikalischer Modelle ist folgender Zusammenhang:
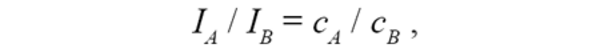
mit: IA/B = Intensität Elementpeak, cA,B = Atomkonzentration Element im Material.
Umgestellt nach der Konzentration des gesuchten Elements A:
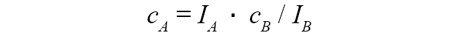
Das physikalische Verhalten von Röntgenstrahlung erfordert nun einen Korrekturfaktor k, welcher sich aus den Beiträgen für die ordnungszahl- bzw. dichteabhängige Wahrscheinlichkeit für Röntgenemission Z, der Absorption A sowie der Fluoreszenz F zusammensetzt [1]:
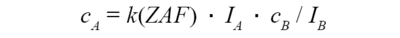
Besonders der Beitrag der Selbstabsorption A in der Probe muss hierbei berücksichtigt werden. Auf diesem Gebiet gibt es bis heute vielfältige Verfeinerungen der Algorithmen, vor allem hinsichtlich der Absorption weicher Röntgenstrahlung (Leichtelementanalyse). Hier wird in der Rasterelektronenmikroskopie gerne die „Phi-Roh-Z“-Korrektur angewandt (Phi = Form der Anregungsbirne, Roh = Materialdichte, Z = Ordnungszahl). Beide Korrekturfaktoren (ZAF sowie Phi-Roh-Z) finden am Phenom proX oder XL mit EDX Verwendung. Um die Beiträge eines Elements zu einem bestimmten Peak quantifizieren zu können, müssen all diese Prozesse von der Software berücksichtigt werden. Hierzu werden Annahmen hinsichtlich homogener Zusammensetzung und einer gleichmäßig ebenen Probenoberfläche gemacht, da-
mit vor allem der dominierende Einfluss der Absorption korrekt berücksichtigt wird. Erfüllt die Probe also nicht die Voraussetzungen, werden die Fehler bei der Quantifizierung in der Regel recht groß. Ein kurzer Exkurs zu den einzelnen Prozessen (siehe auch Abb. 1).
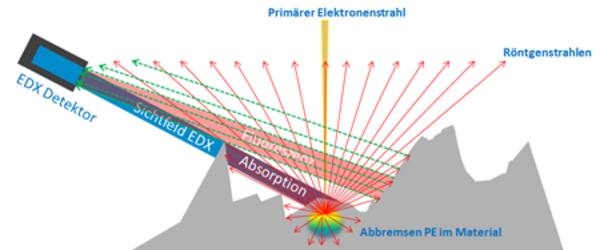
Abb. 1: Vereinfachtes Schema zu wichtigen Prozessen in der EDX
Absorption
Besonders die weiche Röntgenstrahlung wird im Material wieder absorbiert, leichte Elemente bei langen Absorptionswegen unterbestimmt.
Zu beachten sind damit eine starke Topographie, Abschattungen zum Detektor, sowie eine „Deckschicht“ auf dem Material bestehend aus schweren Elementen.
Fluoreszenz
Bei nahe aneinander liegenden Peaks zweier oder mehrerer Elemente ist die höherenergetische Röntgenstrahlung in der Lage, energieärmere Röntgenemission anzuregen. Dadurch verändern sich die Peakintensitäten. Grundsätzlich wird Röntgenfluoreszenz von der Matrixkorrektur berücksichtigt. Dennoch sollte der Benutzer auffällige Intensitätsunterschiede hinterfragen.
Bremsstrahluntergrund
Der reale Bremsstrahluntergrund muss dem berechneten entsprechen. Lädt sich die Probe auf führt der veränderte Untergrund auch zu Fehlern in der Subtraktion desselben.
Besonders schwierig sind quantitative Aussagen über leichte Elemente durch EDX. Da die gemessene Röntgenemission aus oberflächennahen Regionen stammt, wird sie stark durch die Oberflächenchemie der Probe beeinflusst. Leichte Elemente könnten flüchtig sein, so dass sie unterbestimmt werden. Vor allem unedle Metalle oxidieren an der Oberfläche, so dass Sauerstoff überbestimmt wird.In einer der nächsten Ausgaben werden Artefakte im EDX-Spektrum sowie einige spezielle Fälle behandelt.
Quellen
[1] L. Reimer, Scanning Electron Microscopy, Vol. 45, 1998.
Teil I: Good Practice in der Elementanalyse – Stolpersteine der EDX am Rasterelektronenmikroskop
Teil II: Good Practice in der Elementanalyse – Optimierung der REM-Parameter für EDX-Analysen


