Grundlagen – Die Theorie hinter QCM-D
Die QCM-D (Quartz Crystal Microbalance and Dissipation) Technologie basiert auf einem Quarzsensor. Dieser Artikel gibt einen kurzen Überblick über die Historie und beschreibt die dahinter stehenden Grundsätze und mögliche Anwendungsgebiete.
Geschichte
Die Entdeckung des piezoelektrischen Effekts wird Pierre und Jaques Curie zugeschrieben. Diese zeigten im Jahr 1880, dass Kristalle des Rochellesalzes Elektrizität erzeugen können, wenn Druck in bestimmte kristallografische Richtungen ausgeübt wird. [1] Erst Ende der 1950er Jahre begann man jedoch dieses Phänomen systematisch zu erfassen. 1959 veröffentlichte Prof. Dr. Günter Sauerbrey eine Abhandlung in der er zeigte, dass die Frequenzverschiebung von Quarzkristall-Resonatoren (QCR) sich proportional zur veränderten Masse verhält [2]. Sauerbreys Abhandlung war die Geburtsstunde eines neuen Instruments zum Bestimmen sehr kleiner Massen: der Quarzmikrowaage QCM.
Früher wurden alle Messungen in Vakuum oder Gas vorgenommen. Mehrere Forscher stellten Überlegungen an, die Resonatoren in Flüssigkeit zu verwenden. Die Idee wurde aber nicht weiter verfolgt, da man davon ausging, dass Flüssigkeiten die mechanische Schwingung vollständig abdämpfen würde. Im Jahr 1980 zeigten Nomura et al. [3], dass auch ein Kristall, der vollständig in Flüssigkeit getaucht ist, in stabile Schwingungen angeregt werden kann. Dies ermöglichte eine ganze Reihe neuer, nasser Analysemethoden mit dem QCM.
Rodahl untersuchte in seiner Doktorarbeit [4] nicht nur die Resonanzfrequenz eines QCM sondern auch den Verlustfaktor D. Die Kombination aus f und D eröffnete eine Vielzahl neuer Anwendungsfelder. Bisher war es nur möglich zu erfassen, wenn es Änderungen an der starren Masse des Kristalls gab. Nun konnte man auch feststellen, ob das Material starr oder viskoelastisch ist und/oder ob sich die Struktur des Materials verändert.
Unser Partner Q-Sense stellt Schwingquarzmikrowaagen kommerziell zu Verfügung. Sie werden bereits in den unterschiedlichsten Bereichen eingesetzt: Messungen von biochemischen Systemen und Zelladhäsion, Polymerwissenschaften, Reinigungstechnologie und Reinigungsmittel, Arzneimittelentwicklung und viele andere.
Piezoelektrische Resonatoren
Prinzipiell können alle piezoelektrischen Materialien verwendet werden um eine piezoelektrische Mikrowaage herzustellen. Am häufigsten verwendet wird jedoch α-Quarz (im Folgenden vereinfacht Quarz genannt), eine bis 573 °C kristallin stabile Form von Silizium Dioxid (SiO2). Quarzkristalle sind vergleichsweise günstig und einfach herzustellen.
1934 wurde der so genannte AT-Schnitt eingeführt. Durch leichtes Verändern des Schnittwinkels Θ erreicht man, dass die Resonanzfrequenz fast gar nicht temperaturabhängig ist, bei einer gewünschten Temperatur zwischen -60 bis 100 °C (und außerhalb).
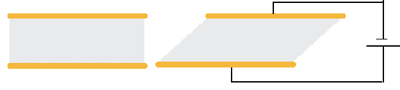
Abb. 1 a Schematische Darstellung der Verformung in einem AT-geschnittenen Kristall
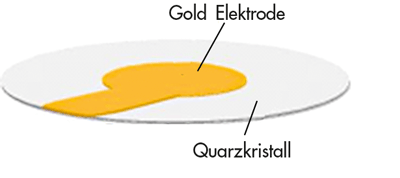
Abb. 1 b Ein Kristall mit Elektrode
Elektroden
Das elektrische Feld wird angelegt, indem ein Paar Elektroden zum Beispiel durch Verdampfen oder Sputtern direkt auf die Hauptflächen des Quarzkristalls aufgebracht wird (s. Abb. 1). Die Elektroden sind in der Regel ca. 100 nm dick.
Grundsätzlich kann jedes elektrisch leitfähige Material, welches sich auf Quarz aufbringen lässt, für die Elektroden verwendet werden. Die gängigsten Elektroden-Materialien sind Al, Ag, und Au.
Massenempfindlichkeit
Sauerbrey hat ein einfaches physikalisches Modell für die beobachtete Proportionalität zwischen der zusätzlichen Masse und der induzierten Frequenzverschiebung vorgestellt [2]. Indem er die Dichte des Quarzes als mq = tqρq definierte, wobei ρq und tq die Dichte, respektive Dicke des Quarzkristalls darstellen, erhielt er
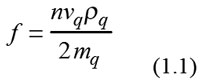
mit n als Wellenanzahl und νq als Wellengeschwindigkeit im Kristall. Durch Differenzieren der Gleichung (1.1) erhielt er
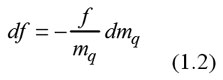
Sauerbrey nahm an, dass bei kleinen Veränderungen in der Masse die zusätzliche Schicht wie eine äquivalente Massenänderung des Kristalls selbst behandelt werden kann. Durch den Austausch von D durch Δ kann die Gleichung also so geschrieben werden
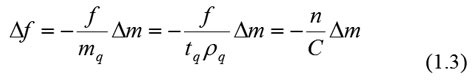
wobei Δm = ρftf, ρf und tf der Dichte und Dicke der zusätzlichen Schicht entsprechen und C die so genannte Massenempfindlichkeit des QCM darstellt. Gleichung (1.3) ist auch als Sauerbrey-Gleichung bekannt.
Bei einem AT-geschnittenen Quarzkristall, mit ρq = 2650 kg/m3 und vq = 3340 m/s [2], liegt die Massenempfindlichkeit für einen 5 MHz-Resonator, der in seinem Grundmode oszilliert, bei 17,7 ng/(cm2Hz1) (n=3 für die dritte Harmonische (15 MHz)). Das bedeutet, dass das Hinzufügen einer Monoschicht Wasser mit einer Masse von ca. 0,25 mg/m2 eine Frequenzverschiebung von –1,4 Hz zur Folge hat. Da die Resonanzfrequenz eines 5 MHz-Kristalls, der in Vakuum schwingt, ganz einfach mit einer Genauigkeit von 0,01 Hz gemessen werden kann, lassen sich auch sehr kleine Massen bestimmen.
Gleichung (1.3) ist anwendbar, wenn die zusätzliche Masse die folgenden Eigenschaften aufweist:
- klein im Vergleich zum Gewicht des Kristalls
- fest
- gleichmäßig über den aktiven Bereich des Kristalls verteilt (s. Abb. 1 a)
Sauerbrey zeigte bei seinen Untersuchungen mit dem QCM, dass die Vibrationen des Kristalls auf den Bereich beschränkt sind, an dem die Elektroden sich überlappen (s. Abb. 2) [5]. Dieser Vibrationsbereich wird auch aktiver Bereich des Kristalls genannt.
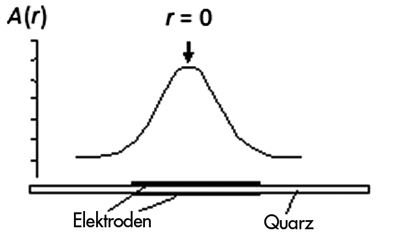
Abb. 2 Schematische Darstellung davon, wie die Vibrationsamplitude A und die differentielle Massenempfindlichkeit S über den Kristall variieren.
Die Vibrationsamplitude A(r) hat ihren Peak in der Mitte der Elektrode r = 0 und fällt zu den Elektrodenenden hin ab. Die Maximalamplitude A(r)max liegt bei ca. 1 zu 10 ηm.
Verlustfaktor
Der Verlustfaktor D ist das Gegenstück zum besser bekannten Gütefaktor Q, der wie folgt definiert wird:
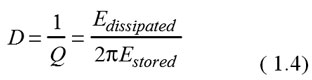
Der Verlustfaktor eines Schwingquarzes kann gemessen werden, indem man das Abklingen der Schwingung aufnimmt. Abb. 3 zeigt eine typische Abklingkurve (zum Beispiel eines elektrischen Signals oder akustischer Wellen). Der Pfeil zeigt an, ab wann der Kristall nicht mehr angeregt wurde.
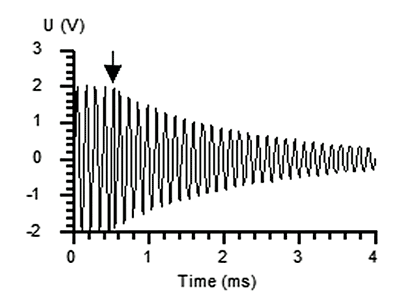
Abb. 3 Typische Abklingkurve
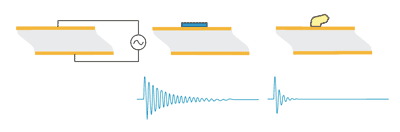
Abb. 4 Schematische Darstellung eines AT-geschnittenen Kristalls in Schwingung mit Abklingkurve bei einer starren (Mitte) und einer viskoelastischen Probe (rechts)
Abb. 4 zeigt schematisch, wie die Abklingkurve sich abhängig von den Eigenschaften des auf den Kristall aufgebrachten Films verändert und verformt.
Referenzen
[1] Curie, P.; Curie, J. C. R Acad. Sci., p 924, (1880) 91
[2] Sauerbrey, G Z. Phys. 155 (1959) 206
[3] Nomura, T.; Hattori, O. Analytica chimica acta 115 (1980) 323
[4] Rodahl, M. On the frequency and Q factor response of the quartz crystal microbalance to liquid overlayers, Ph.D. thesis, Chalmers (1995)
[5] Sauerbrey, G. Archiv der elektrischen Übertragung 18 (1964) 617


