Kleine Einführung: Ellipsometrie

Weitere Informationen

Wenn Licht von einer Materialstruktur reflektiert oder transmittiert wird, ändert sich die Polarisation. Ellipsometrie misst diese Veränderung, die von den optischen Eigenschaften und der Dicke des individuellen Materials abhängen. Ellipsometrie wird in erster Linie dazu benutzt, optische Konstanten und Schichtdicken zu bestimmen, aber auch zur Charakterisierung verschiedener Eigenschaften wie die Zusammensetzung, Kristallinität, Rauheit, Konzentration der Dotierung und anderer Materialeigenschaften, die mit der Veränderung in der optischen Reaktion in Verbindung stehen.

Typische Anwendungsgebiete sind physikalische Grundlagenforschung, Halbleiter- und Datenspeicherungslösungen, Flachbildschirme, Kommunikation, Biosensoren und optische Beschichtungen. Ellipsometrie ist zudem flexibel genug, die meisten Materialtypen zu vermessen: dielektrisches Material, Halbleiter, Metalle, Supraleiter, organisches Material, biologische Beschichtungen und Verbundstoffe.

Polarisiertes Licht

Licht kann als eine elektromagnetische Welle beschrieben werden. Für die Zwecke der Ellipsometrie ist es ausreichend, die Eigenschaft des elektrischen Feldes der Wellen in Raum und Zeit, auch als Polarisation bekannt, zu diskutieren. Das elektrische Feld einer Welle ist stets orthogonal zur Ausbreitungsrichtung. Daher kann eine Welle, die sich entlang der z-Richtung bewegt, durch ihre x- und y-Komponenten beschrieben werden. Licht mit völlig zufälliger Orientierung und Phase gilt es als unpolarisiert. Für die Ellipsometrie sind wir jedoch an der Art des elektrischen Feldes interessiert, das einem bestimmten Weg folgt und an jeder Stelle eine ausgeprägte Form aufweist. Dies wird als polarisiertes Licht bezeichnet. Wenn zwei orthogonale Lichtwellen in Phase sind, ist das resultierende Licht linear polarisiert. Die relativen Amplituden bestimmen die resultierende Orientierung. Sind die orthogonalen Wellen 90 ° phasenverschoben und haben gleiche Amplitude, so ist das resultierende Licht zirkular polarisiert. Die häufigste Polarisation ist "elliptisch" polarisiert: eine Polarisation die orthogonale Wellen beliebiger Amplitude und Phase kombiniert. Hiervon erhält die Ellipsometrie ihren Namen.

Kombinierte orthogonale Wellen, um Polarisation zu demonstrieren:

Lineare Polarisation

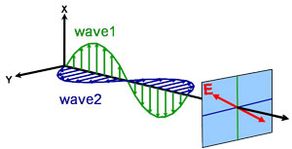
Zirkulare Polarisation

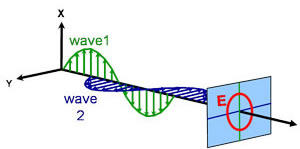
Elliptische Polarisation

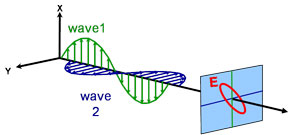
Licht und Material

Zwei Werte werden verwendet, um die optischen Eigenschaften eines Materials zu beschreiben, d.h. wie Licht mit einem Material wechselwirkt. Sie werden im Allgemeinen als komplexe Zahl dargestellt. Der komplexe Brechungsindex (ñ) besteht aus dem Index (n) und dem Extinktionskoeffizienten (k):

Alternativ können die optischen Eigenschaften als die komplexe dielektrische Funktion dargestellt werden:

Mit der folgenden Beziehung zwischen den Konventionen:

Der Index beschreibt die Phasengeschwindigkeit von Licht, wenn es durch ein Material läuft, verglichen mit der Lichtgeschwindigkeit im Vakuum, c:

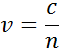
Licht verlangsamt sich, wenn es in ein Material mit höherem Index eintritt. Da die Frequenz der Lichtwellen konstant bleibt, verkürzt sich die Wellenlänge. Der Extinktionskoeffizient beschreibt den Verlust der Wellenenergie an das  Material. Die Beziehung mit dem Absorptionskoeffizienten ist wie folgt:

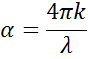
Licht verliert die Intensität in einem absorbierenden Material nach dem Lambert-Beer‘ schen Gesetz:

Somit bezieht sich der Extinktionskoeffizient darauf, wie schnell Licht in einem Material verschwindet. Diese Konzepte werden in Abb. 4 gezeigt, wo eine Lichtwelle durch zwei unterschiedliche Materialien variierender Eigenschaften läuft, bevor sie zur Umgebung zurückkehrt.

Abb. 4 zeigt wie die Lichtwelle durch zwei Materialien unterschiedlicher optischer Eigenschaft läuft bevor sie das Umgebungsmaterial erreicht.

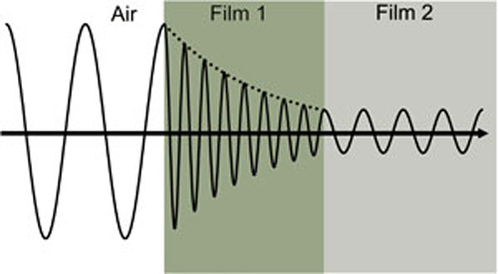
Abb. 4: Die Welle bewegt sich von der Luft in den absorbierenden Film 1 und dann durch den transparenten Film 2. Die Phasengeschwindigkeit und die Wellenlänge ändern sich in jedem Material in Abhängigkeit vom Brechungsindex (Film 1: n = 4, Film 2: n = 2).

Die optischen Konstanten für TiO2 vom Ultraviolett (UV) bis zum Infrarot (IR) sind in Abb. 5 dargestellt. Die optischen Konstanten sind eine Funktion der Wellenlänge, wobei die Absorption (k> 0) sowohl in UV als auch in IR aufgrund von unterschiedlichen Mechanismen auftritt. Die IR-Absorption wird üblicherweise durch molekulare Schwingungen, Phononschwingungen oder freie Ladungsträger verursacht. Die UV-Absorption ist im Allgemeinen auf elektronische Übergänge zurückzuführen, wobei Licht Energie liefert, um ein Elektron zu einem höheren Zustand anzuregen. Ein genauerer Blick auf die optischen Konstanten in Abb. 5 zeigt, dass Real- und Imaginär-Teil der optischen Konstanten nicht unabhängig voneinander sind. Ihre Verläufe sind mathematisch durch die Kramers-Kronig-Konsistenz gekoppelt.

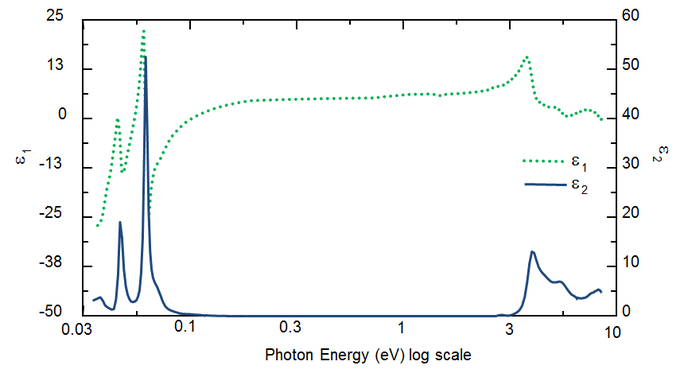
Abb. 5: Komplexe dielektrische Funktion für TiO2-Filme, dargestellt für die Wellenlängen vom Infrarot (niedriges eV) bis zum Ultraviolett (hohes eV).

Wechselwirkung von Licht und Material

Die Maxwell-Gleichungen müssen erfüllt bleiben, wenn Licht mit einem Material wechselwirkt. Dies führt zu Grenzbedingungen an der Oberfläche. Einfallendes Licht wird an der Grenzfläche reflektiert und gebrochen, wie in der folgenden Abbildung gezeigt. Der Winkel zwischen dem einfallenden Strahl und der Probennormale (θ_i) ist gleich dem reflektierten Winkel (θ_r). Licht, das in das Material eintritt, wird in einem Winkel θ_t gebrochen, definiert durch:

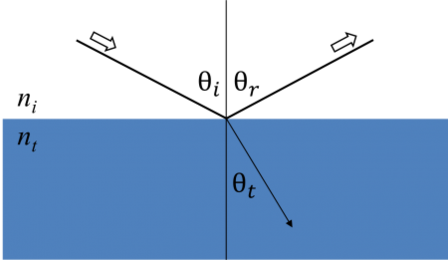
Abb. 6: Licht wird reflektiert und gebrochen entsprechend dem Snellius-Gesetz.

Dasselbe tritt an jeder Grenzfläche auf, an der ein Teil des Lichts reflektiert und der Rest unter dem Brechungswinkel transmittiert. Die Randbedingungen liefern unterschiedliche Lösungen für elektrische Felder parallel und senkrecht zur Probenoberfläche. Daher kann Licht in orthogonale Komponenten in Bezug auf die Einfallsebene getrennt werden. Elektrische Felder parallel und senkrecht zur Einfallsebene werden als p- bzw. s-polarisiert betrachtet. Diese beiden Komponenten sind unabhängig und können separat berechnet werden. Fresnel beschrieb die Lichtmenge, die reflektiert und an einer Grenzfläche zwischen den Materialien übertragen wurde:

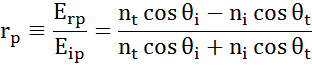
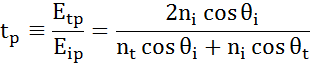
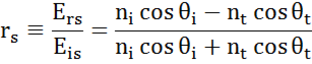
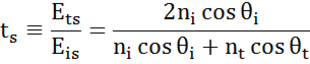
Dünne Filme- und Mehrschichtstrukturen umfassen mehrere Grenzflächen an denen jeweils die Fresnel-Reflexions- und Transmissionskoeffizienten angewendet werden. Es ist wichtig, die relative Phase jeder Lichtkomponente zu verfolgen, um den insgesamt reflektierten oder transmittierten Strahl richtig zu bestimmen. Zu diesem Zweck wird wir die Filmphasendicke wie folgt definiert:

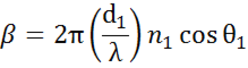
Die Überlagerung mehrerer Lichtwellen führt zu Interferenzen, die von der relativen Phase jeder Lichtwelle abhängen. Die folgende Abbildung zeigt die Kombination von Lichtwellen im reflektierten Strahl und deren entsprechende Fresnel-Berechnungen

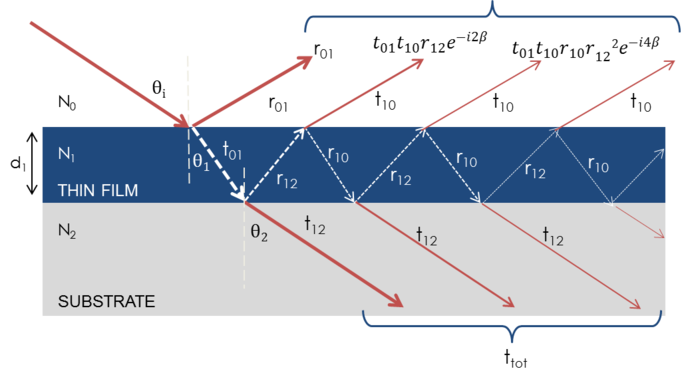
Abb. 7: Licht reflektiert und bricht an jeder Grenzfläche, was zu mehreren Strahlen in einem dünnen Film führt. Die Interferenz zwischen Strahlen hängt von der relativen Phase und der Amplitude der elektrischen Felder ab. Fresnel-Reflexions- und Transmissionskoeffizienten können verwendet werden, um die Antwort von jedem beitragenden Strahl zu berechnen.

Ellipsometrie-Messungen

Die Ellipsometrie ist primär daran interessiert, wie sich p- und s- Komponenten bei Reflexion oder Transmission in Beziehung zueinander ändern. Auf diese Weise ist der Referenzstrahl Teil des Experiments. Eine bekannte Polarisation wird von der Probe reflektiert oder transmittiert, und die resultierende Polarisation wird gemessen. Die Änderung der Polarisation ist die Ellipsometriemessung, die üblicherweise geschrieben wird als:

Eine ellipsometrische Messung an einer Probe ist in Abb. 8 gezeigt. Das einfallende, linear polarisierte Licht besteht sowohl aus einer p- als auch aus einer s- Komponente. Das reflektierte Licht hat Amplituden- und Phasenänderungen sowohl für p- als auch für s-polarisiertes Licht erfahren, und die Ellipsometrie misst diese Änderungen.

Die primär benötigten Elemente zur Aufnahme von Ellipsometriedaten umfassen: Lichtquelle, Polarisationsgenerator, Probe, Polarisationsanalysator und Detektor. Der Polarisationsgenerator und der Analysator sind aus optischen Komponenten aufgebaut, die die Polarisation manipulieren: Polarisatoren, Kompensatoren oder Phasenmodulatoren. Übliche Ellipsometer-Konfigurationen, wie sie für spektroskopische Ellipsometrie eingesetzt werden, sind: rotierender Analysator (RAE), rotierender Polarisator (RPE), rotierender Kompensator (RCE) und Phasenmodulation (PME).

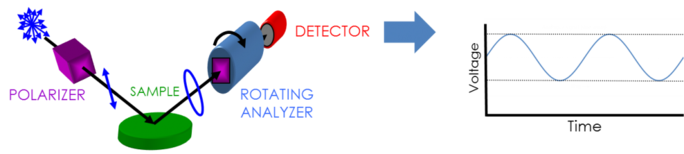
Die RAE-Konfiguration ist in der obigen Abbildung dargestellt. Eine Lichtquelle erzeugt unpolarisiertes Licht, das dann durch einen Polarisator gesendet wird. Der Polarisator ermöglicht, dass Licht einer bevorzugten Ausrichtung des elektrischen Feldes passiert. Die Polarisatorachse ist zwischen der p- und s-Ebene ausgerichtet, so dass beide E-Feldkomponenten an der Probenoberfläche ankommen. Das linear polarisierte Licht reflektiert von der Probenoberfläche, wird elliptisch polarisiert und durchläuft einen kontinuierlich rotierenden Polarisator (der als Analysator bezeichnet wird). Die Lichtmenge, die durchgelassen wird, hängt von der Polarisatororientierung in Bezug auf die elektrische Feld- "Ellipse", beeinflusst von der Probe, ab. Der Detektor wandelt Licht in ein elektronisches Signal um, worüber die reflektierte Polarisation bestimmt wird. Diese Information wird mit der bekannten Eingangspolarisation verglichen, um die durch die Probenreflexion verursachte Polarisationsänderung zu bestimmen. Dies ist die Ellipsometrie-Messung zur Bestimmung von Psi und Delta.

Ellipsometrische Datenauswertung

Die Ellipsometrie misst die Änderungen der Lichtpolarisation, um daraus die interessierenden Probeneigenschaften, wie Filmdicke und optische Konstanten, zu bestimmen. Im Fall einer Volumenprobe (bulk) können die für eine einzelne Reflexion abgeleiteten Gleichungen direkt invertiert werden, was die "pseudo" optischen Konstanten aus der Ellipsometrie-Messung liefert:

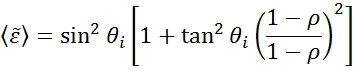
Bei dieser Gleichung wird angenommen, dass es keine Oberflächenschichten jeglicher Art gibt. Jedoch gibt es bei nahezu jeder Bulkprobe typischerweise ein Oberflächenoxid oder eine Oberflächenrauigkeit, und die direkte Inversion würde diese als Teil der optischen Volumenkonstanten enthalten.

Das allgemeinere Verfahren, das verwendet wird, um Materialeigenschaften aus Ellipsometriemessungen abzuleiten, folgt dem Flußdiagramm in Abb. 10. Eine Regressionsanalyse ist erforderlich, da eine exakte Gleichung nicht geschrieben werden kann. Oft ist die Antwort mit Hunderten von experimentellen Datenpunkten für einige Unbekannte überbestimmt. Die Regressionsanalyse erlaubt es, alle gemessenen Daten bei der Bestimmung der Lösung einzubeziehen.

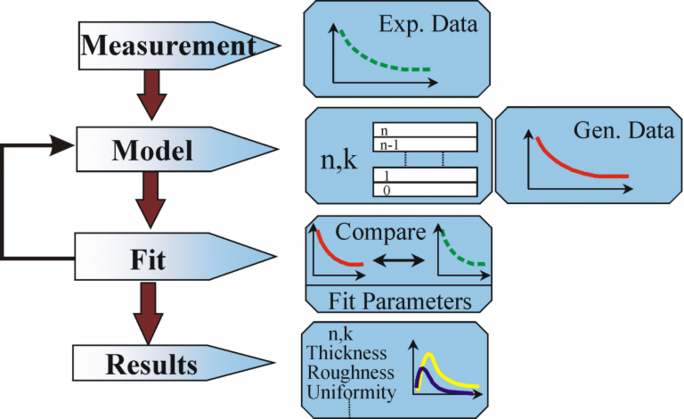
Abb. 10: Flussdiagramm zur ellipsometrischen Datenauswertung

Die Datenanalyse verläuft wie folgt: Nachdem eine Probe gemessen wurde, wird ein Modell zur Beschreibung der Probe erstellt. Dieses Modell wird verwendet, um die vorhergesagte Antwort aus den Fresnel´schen Gleichungen zu berechnen, die jedes Material mit Dicke und optischen Konstanten beschreiben. Sind diese Werte nicht bekannt, erfolgt eine Annahme für die Kalkulation. Die berechneten Werte werden mit experimentellen Daten verglichen. Alle unbekannten Materialeigenschaften können dann variiert werden, um die Übereinstimmung zwischen Experiment und Berechnung zu verbessern. Die Anzahl der unbekannten Parameter sollte die in den experimentellen Daten enthaltenen Informationen nicht übersteigen. Beispielsweise liefert ein Einwellenlängen-Ellipsometer zwei Datenpunkte (Ψ, Δ), die es ermöglichen, maximal zwei Materialeigenschaften zu bestimmen, d.h. nach zwei unbekannten Parametern zu fitten (z.B. n und Dicke). Das Finden der besten Übereinstimmung zwischen dem Modell und dem Experiment wird typischerweise durch Regression erreicht. Dabei wird der Mean Squared Error (MSE) verwendet, um die Differenz zwischen gemessenen und berechneten Kurven zu quantifizieren. Die unbekannten Parameter werden so lange variiert, bis der minimale MSE erreicht ist.

Die beste Antwort entspricht dem niedrigsten MSE. Beispielsweise zeigt die folgende Abbildung die MSE-Kurve gegenüber der Filmdicke für einen transparenten Film auf Silizium. Es gibt mehrere "lokale" Minima, aber der niedrigste MSE-Wert tritt bei einer Dicke = 749 nm auf. Dies entspricht der korrekten Schichtdicke. Es ist möglich, dass der Regressionsalgorithmus fälschlicherweise in ein "lokales" Minimum fällt, abhängig von der Ausgangsdicke und den MSE-Strukturbedingungen. Ein Vergleich der Ergebnisse mit dem Auge für den niedrigsten MSE und für ein lokales Minimum ermöglicht es Ihnen, das wahre globale Minimum leicht zu erkennen.

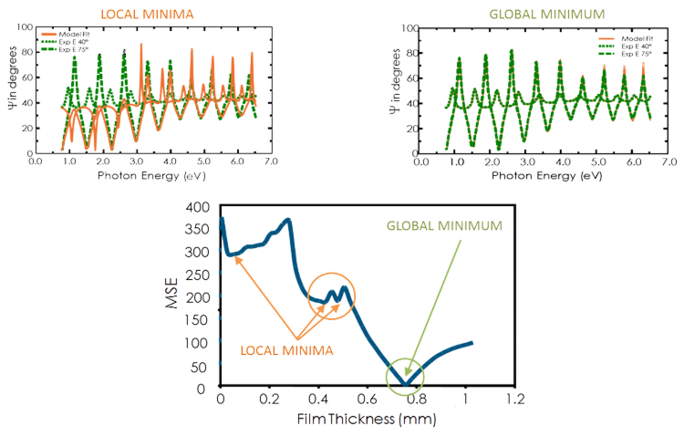
Abbildung 11, unten:  MSE-Kurve versus Dicke zeigt das "globale" Minimum. "Lokale" Minima können durch den Regressionsalgorithmus gefunden werden, ergeben aber nicht das Endergebnis. Abbildung 11, oben rechts: Die experimentellen Daten und entsprechende Kurven, die für das Modell basierend auf dem "globalen" Minimum erzeugt wurden. Abbildung 11, oben links: Eine ähnliche Kurve am "lokalen" Minimum in der Nähe von 0,45 Mikron Dicke ist leicht als fehlerhaftes Ergebnis zu erkennen.

Schichtdicke

Die Schichtdicke wird über die Interferenz zwischen reflektiertem Licht an Schichtoberfläche und der unteren Schichtgrenzfläche bestimmt. Abhängig von der relativen Phase des aus der Schicht kommenden Lichts zur Oberflächenreflexion können Interferenzen als konstruktiv oder destruktiv definiert werden. Die Interferenz umfasst sowohl Amplituden- als auch Phaseninformationen. Die Phaseninformation von Δ ist sehr empfindlich gegenüber Schichten bis runter zu Submonolagendicke. Die Abbildung unten vergleicht die Messungen von reflektierter Intensität und Spektralellipsometrie für die gleiche Serie von dünnen SiO₂ -Schichten auf Si. Die geringe Schichtdicke verursacht große Änderungen in Δ, während das Reflexionsspektrum für jeden Film nahezu gleich ist.

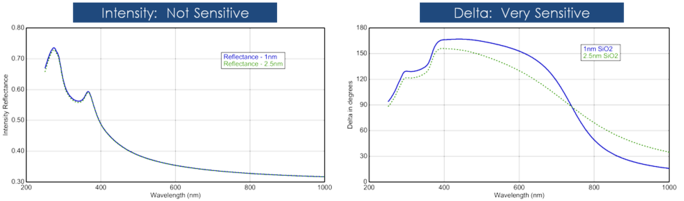
Abb 12, links: Reflektierte Intensität und (rechts) ellipsometrisches Delta für zwei dünne Oxide auf Silizium zeigen die hohe Schichtdickenempfindlichkeit von Delta im nm-Bereich für Schichten, die mit Reflexionsintensität nicht auflösbar sind.

Die spektrokopische Ellipsometrie wird typischerweise für Schichten verwendet, deren Dicke von Sub-Nanometer bis zu einigen Mikrometern reicht. Wenn Filme dicker als einige zehn Mikron werden, werden Interferenzoszillation immer schwieriger aufzulösen zu sein, außer man erweitert den Spektralbereich zu längeren Infrarotwellenlängen. Ansonsten müssen andere Charakterisierungsmethoden verwendet werden.

Dickenmessungen erfordern auch, dass ein Teil des Lichts durch den gesamten Film läuft und an die Oberfläche zurückkehrt. Wenn das Material Licht absorbiert, sind die Dickenmessungen durch optische Instrumente auf dünne, halb-opake Schichten beschränkt. Diese Einschränkung kann adressiert werden, indem die Messungen in einem Spektralbereich mit geringerer Absorption erfolgen. Beispielsweise kann ein organischer Film stark UV- und IR-Licht absorbieren, aber bei mittleren sichtbaren Wellenlängen transparent bleiben. Für Metalle, die bei allen Wellenlängen stark absorbieren, beträgt die maximale Schichtdicke zur Dickenbestimmung typischerweise etwa 100 nm.

Optische Konstanten

Dickenmessungen sind nicht unabhängig von den optischen Konstanten. Die Filmdicke beeinflusst die die optische Weglänge des durch den Film verlaufenden Lichtes, aber der Index bestimmt die Geschwindigkeit der Lichtwellen und den Beugungswinkel. Somit tragen beide zur Verzögerung zwischen Oberflächenreflexion und Licht, das durch die Schicht läuft, bei. Sowohl n als auch k müssen bekannt sein oder zusammen mit der Dicke bestimmt werden, um die korrekten Ergebnisse einer optischen Messung zu gewährleisten.

Die optischen Konstanten eines Materials variieren als Funktion der Wellenlänge und müssen somit für alle Wellenlängen beschrieben werden, bei denen mit dem Ellipsometer gemessen wird. Eine Tabelle mit optischen Konstanten kann verwendet werden, um die Antwort des Materials bei jeder Wellenlänge vorherzusagen. Jedoch ist es nicht sehr sinnvoll, unbekannte optische Konstanten Wellenlänge für Wellenlänge anzupassen. Sinnvoller ist es, alle Wellenlängen gleichzeitig mittels einer Dispersionsfunktion anzupassen. Eine Dispersionsbeziehung liefert eine physikalische Beschreibung der optischen Konstanten als Funktion der Wellenlänge. Die anpassbaren Parameter der Dispersionsbeziehung ermöglichen den kompletten Wellenlängenverlauf der gesamten optischen Konstanten mit an die experimentellen Daten anzupassen. Verglichen mit der Anpassung einzelner n, k-Werte bei jeder Wellenlänge reduziert dies deutlich die Anzahl der unbekannten "freien" Parameter.

Für transparente Materialien wird zur Beschreibung des Brechungsindex häufig die Cauchy- oder Sellmeier-Beziehung verwendet. Die Cauchy-Dispersion wird typischerweise wie folgt definiert:

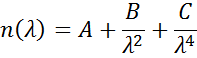
Wobei die drei Terme so beschrieben werden, daß sie dem Brechungsindex des Materials entsprechen. Die Cauchy-Funktion ist nicht durch KK-Konsistenz bedingt und kann unphysikalische Dispersion erzeugen. Die Sellmeier-Beziehung erzwingt Kramers-Kronig-Konsistenz (KK), die dafür sorgt, dass die optische Dispersion eine realistische Form behält. Die Sellmeier-Beziehung kann wie folgt geschrieben werden:

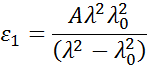
Absorbierende Materialien weisen oft einen transparenten Wellenlängenbereich auf, der mit dem Cauchy oder Sellmeier modelliert werden kann. Der absorbierende Bereich muss jedoch sowohl reale als auch imaginäre optische Konstanten berücksichtigen. Viele Dispersionsbeziehungen verwenden die Oszillatortheorie, um die Absorption für verschiedene Materialien zu beschreiben. Dazu gehören die Lorentz-, Harmonic- und Gaussian-Oszillatoren. Sie weisen alle ähnliche Eigenschaften auf, wobei die Absorptionsmerkmale mit Amplitude, Verbreiterung und Mittenenergie (bezogen auf Frequenz des Lichts) beschrieben sind. Kramers-Kronig-Konsistenz wird verwendet, um die Form der realen Komponente zu berechnen, nachdem das imaginäre Verhalten durch den Oszillator beschrieben wurde. Ein Offset zur realen Komponente wird addiert, um zusätzliche Absorption außerhalb des gemessenen Spektralbereichs zu berücksichtigen. Der Lorentz-Oszillator kann wie folgt geschrieben werden:

die Parameter für Amplitude (A), Verbreiterung (B), Mittelenergie (Ec) und Offset (e1, off set) sind in Abb. 13 für einen typischen Lorentz-Oszillator dargestellt. Die Energie E bezieht sich auf die Frequenz des Lichts:

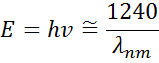
wobei h die Planck´sche Konstante und die Wellenlänge λ in Nanometer angegeben ist. Weiterentwickelte Dispersionsmodelle, wie Tauc-Lorentz und Cody-Lorentz, enthalten zusätzliche Terme zur Beschreibung der Bandlückenenergie.

Zusätzliche Literatur

Die Ellipsometrie ist eine gängige optische Methode zur Messung von dünnen Schichten und Bulkproben. Sie beruht auf den Polarisationsänderungen, die durch Reflexion oder Transmission von einer Materialstruktur verursacht werden, um daraus die Materialeigenschaften wie die Dicke und die optischen Konstanten abzuleiten. Diese Technik entwickelt sich weiter, da die Nachfrage nach Dünnschichtcharakterisierung weiter zunimmt.

Aspnes D.E. (1985). The Accurate Determination of Optical Properties by Ellipsometry. In: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. and Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, The Netherlands.

Boccara A.C., Pickering C., and Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E., and Irene E.A. (eds.), (1998). “Proceedings from the Second International Conference on Spectroscopic ellipsometry”. In: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T., and Redondo A. (1995). “Recent applications of ellipsometry and spectroellipsometry in electrochemical systems”, In: I. Rubinstein (ed.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, California.

Johs B. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications”. Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). “Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.

Rossow U. and Richter W. (1996). “Spectroscopic Ellipsometry” in: Bauer G and Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.

Tompkins H.G. and McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.

Tompkins, H.G. and Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. and Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. and Snyder P.G. (1992). “Variable Angle Spectroscopic Ellipsometry” in: Brundle CR, Evans CA, and Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications”. Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). “Ellipsometry, Variable Angle Spectroscopic” in: Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.

Kontakt