Einführung in die Breitband-FMR-Spektroskopie Teil 2 – Versuchsaufbau
Magnetisierungsdynamik - Landau-Lifshitz-Gilbert-Gleichung
Die in Abbildung 1 dargestellte Landau-Lifshitz-Gilbert (LLG)-Gleichung [2] zeigt die klassische Beschreibung der Mikrowellenmagnetisierungsdynamik.
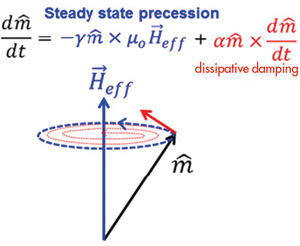
Abb. 1 Magnetisierungsdynamik, wie sie in der Landau-Lifshitz-Gilbert-Gleichung beschrieben ist
Der Magnetisierungsvektor γ ist dabei das gyromagnetische Verhältnis, μo ist die Permeabilität des freien Raumes, Heff das wirkende Magnetfeld und α der phänomenologische Gilbert-Dämpfungskoeffizient. Der Begriff in blau beschreibt die stationäre Präzession des Magnetisierungsvektors um Heff.
In Abwesenheit von viskosen Kräften würde der Magnetisierungsvektor auf unbestimmte Zeit entlang der in Abbildung 1 dargestellten gestrichelten blauen Trajektorie präzedieren. Dissipative Kräfte führen jedoch dazu, dass die Magnetisierung nach innen hin spiralförmig zuläuft. Diese sind durch die rote punktierte Trajektorie dargestellt und kollinear zu Heff. Sie werden durch den phänomenologischen Gilbert-Dämpfungskoeffizienten α quantifiziert.
Mit einem FMR-Spektrometer lässt sich diese Magnetisierungsdynamik sowohl stimulieren als auch messen.
Versuchsaufbau
Das Herz eines breitbandigen FMR-Spektroskopie-Messaufbaus (Abb.2 (a)) ist der koplanare Wellenleiter (CPW). CPWs sorgen für die effiziente Übertragung eines Mikrowellensignals von einer Hochfrequenzquelle (RF) über einen breiten Frequenzbereich. Die CPWs von NanOsc Instruments können Frequenzen von 2-40 GHz übertragen.
In unmittelbarer Nähe zum CPW wird ein Mikrowellen-HF-Magnetfeld (HRF) erzeugt, das bei einem geeigneten Magnetfeld (HDC) und geeigneter Frequenz eine Magnetprobe resonant anregen kann. Da die HF-Magnetfelder nur eine sehr geringe Reichweite haben, ist es wichtig, dass die magnetischen Filme auf dem CPW auf die Folienseite gelegt werden, um die Kopplung und das resultierende Signal zu maximieren. Es ist auch wichtig, dass die Probe den CPW nicht ausschaltet. Daher wird häufig eine dünne Isolierschicht (z.B. gesputtertes SiOx oder spinbeschichteter Photoresist) auf der Probe abgeschieden. Man kann auch eine einzelne Schicht aus transparentem Klebeband auf den CPW legen, um eine isolierende Barriere zu schaffen. HRF sollte senkrecht zu HDC sein, wie in Abbildung 2(a) gezeigt, da dies den effizientesten Anregungsmechanismus darstellt.
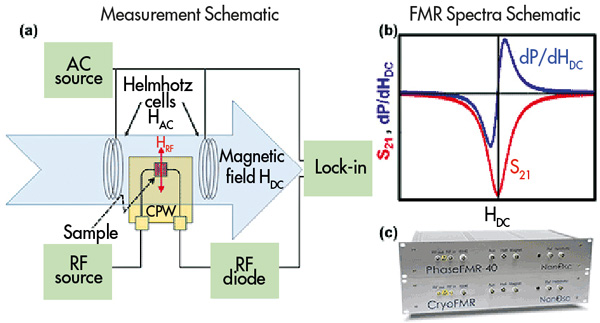
Abb. 2 (a) Schematische Breitband-FMR-Messeinrichtung, die die kritischen Komponenten hervorhebt (b) Schematische Messspektren (c) NanOsc FMR-Spektrometer
Messungen werden typischerweise mit einer festen Frequenz durchgeführt, während HDC variiert wird. So wird die dominante frequenzabhängige Hintergrundantwort eliminiert, die die relativ schwache FMR-Antwort der Probe maskieren kann. Da HDC durch den Resonanzzustand kontinuierlich durchgestimmt wird, beginnt die Magnetisierung resonant zu präzedieren und Energie vom CPW zu absorbieren. Diese Abnahme der übertragenen HF-Energie beim Erreichen des Resonanzfeldes wird durch eine Breitband-HF-Diode in eine Gleichspannung umgewandelt. Eine solche schematische S21-Absorptionsantwort ist durch die rote Kurve in Abbildung 2(b) dargestellt. Um das Signal-Rausch-Verhältnis (SNR) zu verbessern, wird häufig eine Lock-In-Detektionstechnik verwendet, die das Modul mit einer bekannten Frequenz moduliert. Diese Modulation wird durch einen zusätzlichen Satz von Helmholtz-Spulen ermöglicht. Diese werden von einer Wechselstromquelle angetrieben, die im Gegenzug eine kleine (~1 Oe) Modulation (HAC) zu der viel größeren HDC erzeugt. Daher wird mit diesem modifizierten Messschema tatsächlich die Ableitung der übertragenen Leistung (dP/dHDC) gemessen, die schematisch in Abbildung 2(b) blau dargestellt ist. Die in Abbildung 2(a) gezeigten elektronischen Komponenten (AC-Quelle, HF-Quelle, HF-Diode und Lock-In) sind zusammen mit der zur Steuerung erforderlichen Elektronik bequem in dem FMR-Spektrometer von NanOsc (2(c)) untergebracht. Über einen kalibrierten Hall-Sensor wird das Magnetfeld bestimmt.
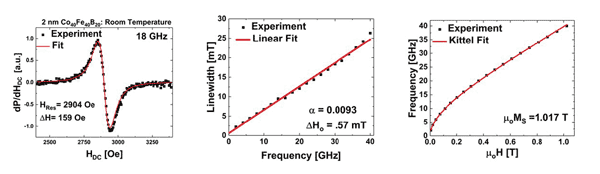
Abb. 3 (a) Experimentelles Resonanzspektrum (schwarze Quadrate) mit Fit (rote Linie), um das Resonanzfeld und die Linienbreite bei f = 6 GHz für einen 2 nm dicken Co40Fe40B20-Film zu extrahieren. Das extrahierte (b) Resonanzfeld und (c) die Linienbreite als schwarze Quadrate über den Frequenzbereich von 2 bis 40 GHz, zusammen mit den zugehörigen Anpassungen (rote Linien), die zur Berechnung von μoMS, ΔHo und α verwendet werden
Anpassung der Resonanzspektren: Extrahieren von Resonanzfeld und Linienbreite
Ein typisches experimentelles Resonanzspektrum, gemessen für einen 2 nm dicken Co40Fe40B20-Film bei einer Resonanzfrequenz von 6 GHz, ist in Abbildung 3(a) (schwarze Quadrate) als eine Funktion des in der Ebene liegenden Magnetfeldes gezeigt. Die experimentellen Daten wurden dann mit Hilfe der FMR-Spektrum-Fit-Gleichung gefittet (3 (a) rote Linie), die in Abbildung 2(a) gezeigt ist, um das Resonanzfeld (Hres) und die Linienbreite (ΔH) bei einer bestimmten Frequenz zu extrahieren. Diese Gleichung berücksichtigt die Belastung des CPWs beim Durchlaufen der Resonanzbedingung und ist daher keine einfache Ableitung einer Lorentzschen Funktion [3]. Die Funktion berücksichtigt auch kleine lineare Hintergründe und vertikale Offsets. Die extrahierten Hres und ΔH für Frequenzen bis zu 40 GHz sind in Abbildung 3(b) bzw. (c) dargestellt.
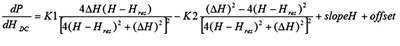
Abb.4 FMR-Spektrum und Datenfitgleichung
Die Gleichung, die verwendet wird, um die Daten zu fitten und μoMS, ΔHo und α zu extrahieren, siehe Abb. 4.
Im nächsten und letzten Teil zeigen wir Ihnen Messbeispiele für unterschiedliche Dünnfilme. Dabei beschreiben wir auch temperaturabhängige Messungen und inverse Spin-Hall-Effekt (ISHE)-Messungen.
Quellen
[2] A. Gurevich and G. Melkov, “Magnetization oscillations and waves”, CRC Press, Boca Raton, 1996
[3] G. Woltersdorf, Ph.D. thesis, Simon Fraser University, 2004


