Woollam-Newsletter – Ausgabe 21 ist erschienen
Der neue Newsletter von Woollam ist da. In Ausgabe 21 finden Sie wieder interessante Artikel zum Thema spektroskopische Ellipsometrie. Ein Artikel behandelt ausführlich die Möglichkeiten und Leistungsfähigkeit der Transmission Mueller Matrix-Ellipsometrie.
Weitere Themen:
- Ein Interview mit Hans Arwin (sein Leben mit der Ellipsometrie und der Freude am Lesen)
- Portrait: Prof. Maurizio Canepa, Universität Genua
Im Artikel „Ellipsometrie an flexiblen polarisierenden Substraten“ stellen wir interessante Fallstudien vor, die die Leistungsfähigkeit der spektroskopischen Ellipsometrie für flexible Substrate und deren Geräte zeigen.
Einführung
Moderne Elektronik wird immer dünner, leichter, anpassungsfähiger, biegsamer oder rollbar. Sie können Ihr Smartphone jetzt so falten, dass es in kleine Taschen passt. Sie können Ihre elektronischen Geräte tragen, um Ihre E-Mails abzurufen oder Ihre tägliche körperliche Aktivität zu überwachen. Geräte für erweiterte, virtuelle und gemischte Realität (AR/VR/MR) ermöglichen es Ihnen, eine fesselnde virtuelle oder fiktive Realität zu erleben, z. B. über den Eiffelturm zu fliegen oder virtuelle Monster in Ihrem Hinterhof zu fangen. Die J.A. Woollam Company hat in letzter Zeit viele Anfragen zur Charakterisierung von flexiblen Substraten, wie flexiblem Glas, Polymerplatten, Metallfolien und sogar flexibler Keramik erhalten, da diese Industrien wachsen.
Flexible polarisierende Elemente
Die Ellipsometrie misst die Änderung der Lichtpolarisation, die durch eine Probe unter einem Messwinkel hervorgerufen wird. Wenn die Probe so konstruiert ist, dass sie die Eingangspolarisation in einer bestimmten Weise verändert, können ellipsometrische Messungen den Polarisationseffekt oft ohne strenge Modellierung bewerten. Wir werden zunächst drei verschiedene flexible, polymere optische Elemente betrachten, die häufig in optischen Geräten verwendet werden, um Phasenverschiebungen zu erzeugen oder Strahlen zu filtern, um lineare oder zirkulare Polarisationen zu erzeugen. Wir werden nützliche Softwarefunktionen vorstellen, um zu demonstrieren, wie die spektroskopische Ellipsometrie die polarisierenden Eigenschaften der Probe wie Retardanz, polarisationsabhängige Intensitäten, Azimut und Elliptizität bestimmt.
1. Linearer Retarder
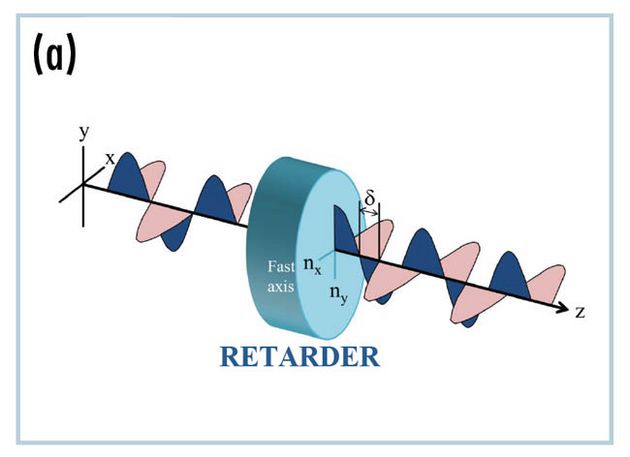
Ein linearer Retarder verzögert eine Komponente eines elektrischen Feldes relativ zu einer anderen orthogonalen Komponente, wodurch eine Phasenverschiebung (δ) zwischen zwei orthogonalen, linearen Polarisationen entsteht. Die Phasenverschiebung wird durch den Indexunterschied des linearen Retarders zwischen den beiden orthogonalen Richtungen verursacht, wie in Abb. (a) dargestellt. Die Phasenverschiebung wird in Grad, Wellen, Bogenmaß oder Nanometern angegeben und oft als Retardance bezeichnet. Das gebräuchlichste optische Element, das die Retardance erzeugt, ist eine Wellenplatte. Eine Viertelwellenplatte ist beispielsweise so konstruiert, dass sie einen Retardancewert von 90⁰ erzeugt, und eine Halbwellenplatte ist so konstruiert, dass sie einen Retardancewert von 180⁰ erzeugt.
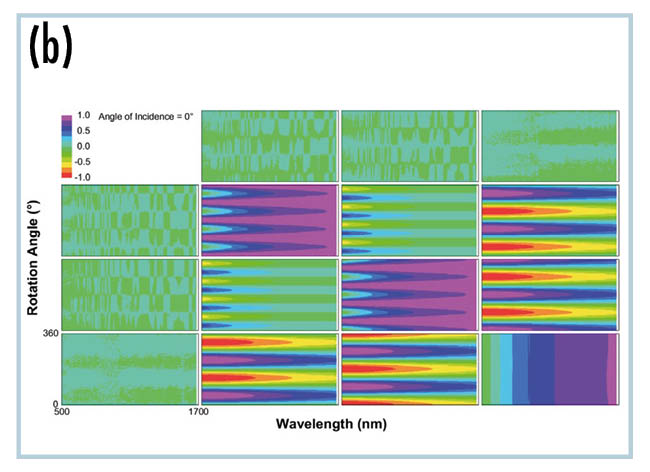
Abb. (b) zeigt die Daten der spektroskopischen Mueller-Matrix-Ellipsometrie für Licht, das senkrecht durch einen dünnen Polymerfilm (~75 µm) hindurchgeht. Die x-Achse ist der Wellenlängenbereich und die y-Achse ist der Drehwinkel um die Probennormale. Der Polymerfilm ist optisch biaxial, wodurch eine Phasenverschiebung zwischen der x- und der y-Richtung entsteht. Der Effekt der linearen Verzögerung füllt den unteren rechten 3×3-Block der Mueller-Matrix aus.
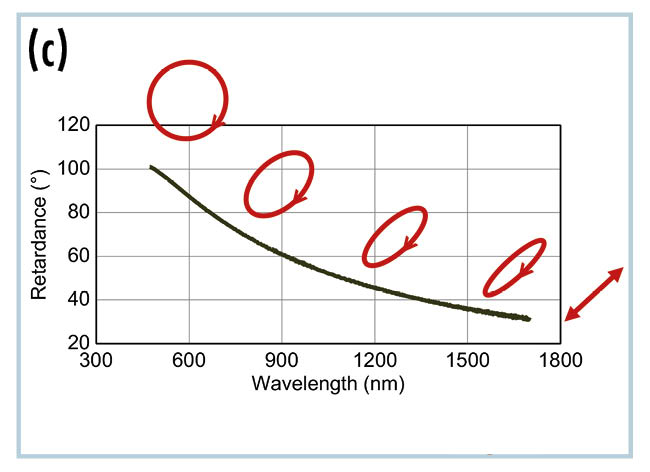
Das Retardancemodell in unseren Softwareprogrammen CompleteEASE und WVASE bietet eine einfache Lösung zur Charakterisierung linearer Retarder. Es verwendet Matrixdiagonalisierungsalgorithmen zur Extraktion der linearen Retardance aus verallgemeinerten spektroskopischen Ellipsometriedaten. Die wellenlängenabhängige Retardance des Polymerfilms wird aus dem Retardancemodell in Abb. (c) extrahiert. Die resultierende Polarisation ist in rot eingezeichnet, um die Wirkung des Retarders auf eine einfallende lineare 45⁰-Polarisation zu veranschaulichen. Das Ergebnis zeigt, dass die Retardance linear polarisiertes Licht in elliptisch polarisiertes Licht umwandelt. In der Nähe von 500 nm wirkt die Polymerfolie wie eine Viertelwellenplatte, und die lineare Polarisation wird in zirkulare Polarisation umgewandelt. Die Retardance wird durch den Indexunterschied multipliziert mit der Weglänge durch den Retarder bestimmt. Daher ist die Anpassung der Dicke der Polymerfolie eine bequeme Methode, um eine Viertel- (oder Halb-) Wellenplatte bei einer bestimmten Wellenlänge zu erzeugen.
2. Linearer Polarisator
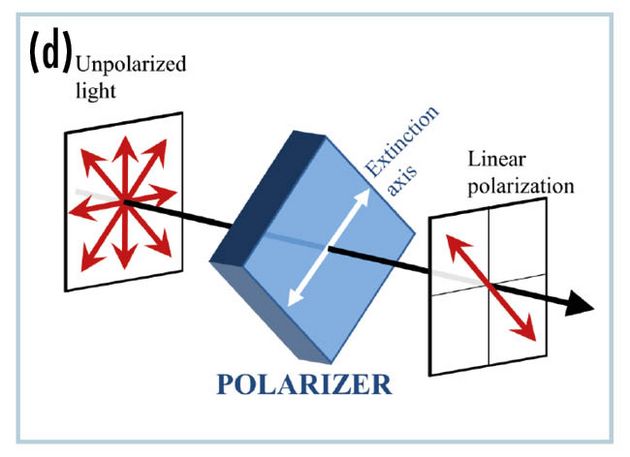
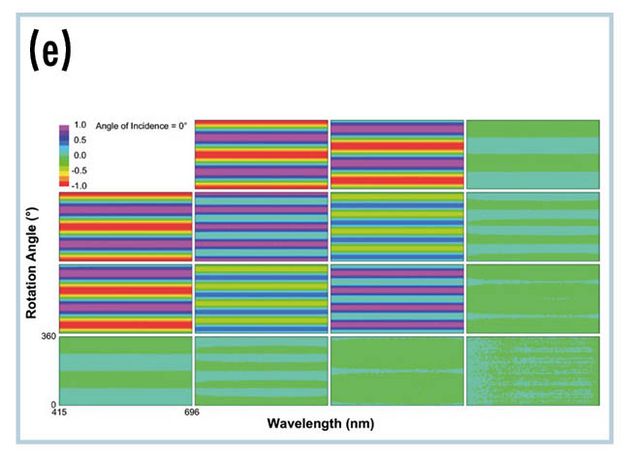
Lineare Polarisatoren werden häufig in Sonnenbrillen, Kamerafiltern, Fensterbeschichtungen oder Anzeigegeräten verwendet. Sie übertragen das parallel zur Transmissionsachse schwingende elektrische Feld und absorbieren das orthogonale elektrische Feld, das parallel zur Extinktionsachse verläuft, wie in Abb. (d) dargestellt. Diese richtungsabhängige Intensitätsabschwächung wird als Dichroismus bezeichnet. Der lineare Dichroismus füllt den oberen linken 3×3-Block der Mueller-Matrix aus (e).
Wie das Retardancemodell bietet auch der von der Mueller-Matrix abgeleitete Parameter in der CompleteEASE-Software eine bequeme Möglichkeit zur Extraktion nützlicher Parameter für optische Elemente, einschließlich linearer Polarisatoren. Diese Funktion berechnet die resultierenden Stokes-Parameter auf der Grundlage der benutzerdefinierten Eingangspolarisation. Als Ergebnis kann der Benutzer auf nützliche Polarisations- oder Depolarisationsparameter wie Azimut, Elliptizität, Polarisationsgrad, % Depolarisation und polarisationsabhängige Intensitäten zugreifen.
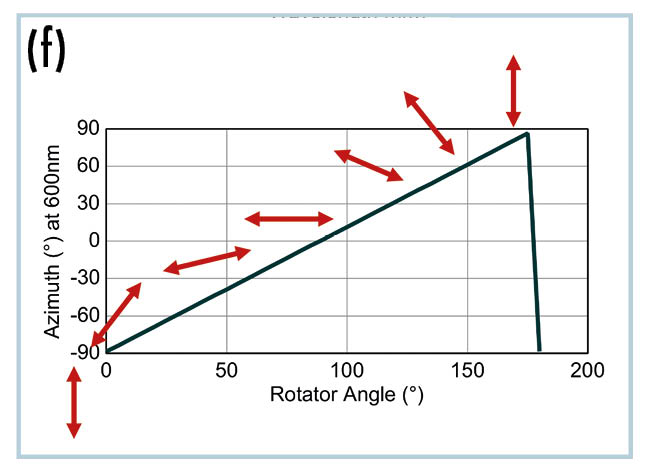
Abb. (f) zeigt den abgeleiteten azimutalen Winkel der transmittierten Polarisation durch einen 94 µm dicken Polymerpolarisator, während er sich um die Probennormale dreht. Die Messung des Azimutwinkels und der Elliptizität ohne zusätzliche optische Elemente, wie z. B. einen weiteren Polarisator oder eine Viertelwellenplatte, ist von Vorteil, um die Leistung und Gleichmäßigkeit des Polarisators in einem Gerät zu überwachen.
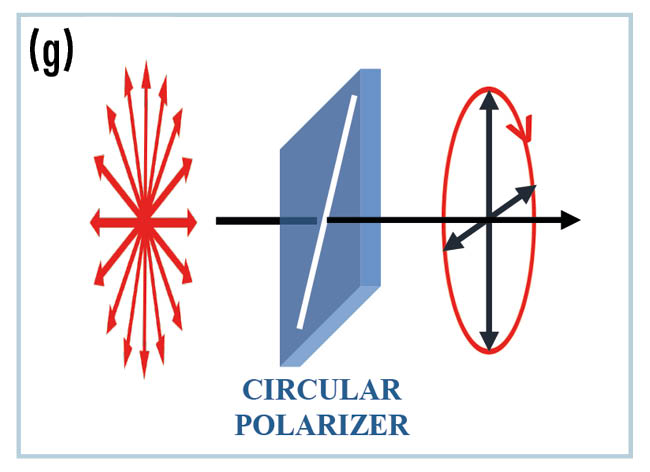
3. Zirkularer Polarisator
Das dritte optische Element ist ein zirkularer Polarisator, der aus zwei in Reihe geschalteten flexiblen Polymerfolien besteht: einer Viertelwellenplatte und einem linearen Polarisator. Ein solches Objekt zeigt je nach Lichtrichtung unterschiedliche optische Reaktionen und ellipsometrische Messdaten. Wir bezeichnen es als inhomogenes optisches Element, das nicht orthogonale Eigenpolarisationen erzeugt.
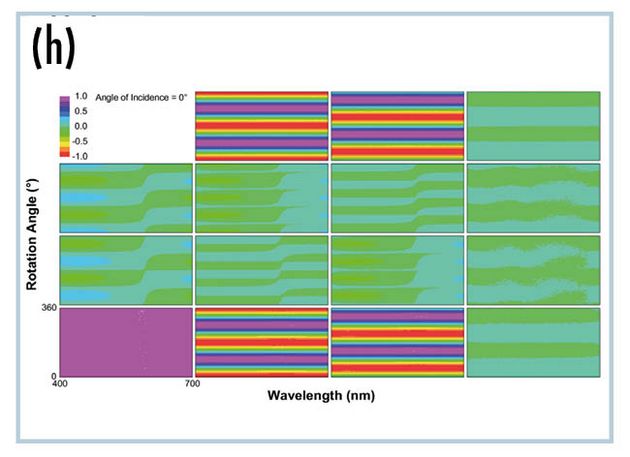
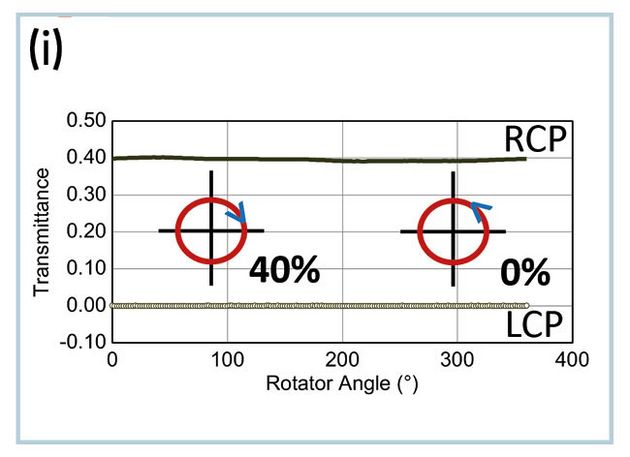
Objekts in Vorwärtsrichtung, wenn der Strahl zuerst in den linearen Polarisator und dann in die Viertelwellenplatte eintritt. Die schnelle Achse der Viertelwellenplatte ist um 45⁰ gegenüber der Transmissionsachse des linearen Polarisators gedreht. Im Gegensatz zu homogenen optischen Elementen weist die resultierende Mueller-Matrix kein symmetrisches Verhalten auf. Diese Vorwärtsrichtung wandelt unpolarisiertes Licht in zirkular polarisiertes Licht um, das als Zirkularpolarisator verwendet wird. Das m41 Mueller-Matrix-Element (=1) in Abb. (h) zeigt den zirkular polarisierenden Effekt. Abb. (i) zeigt den aus der Mueller-Matrix abgeleiteten Transmissionsgrad für jede zirkulare Polarisation. Zwanzig Prozent des Lichts werden von der Oberfläche reflektiert. Von dem verbleibenden Licht geht die Hälfte (40 %) durch das Gerät und wird zu rechtszirkular polarisiertem Licht polarisiert, die andere Hälfte wird absorbiert. Zirkularpolarisatoren werden vor Kameraobjektiven eingesetzt, um bessere fotografische Bilder zu erhalten. Obwohl hier nicht gezeigt, filtert die umgekehrte Richtung eingehendes zirkular polarisiertes Licht entsprechend seiner Händigkeit und ermöglicht so interessante optische Geräte wie stereoskopische 3D-Brillen .
Den vollständigen Artikel finden Sie im Woollam Newsletter 21, der in Kürze auch bei uns erscheinen wird.
Ansprechpartner
| +49 6157 80710-68 | |
| +49 6157 80710968 | |
| E-Mail schreiben |