Why are there no high-resolution gratings for the IR range?
Have you ever asked yourself why high-resolution gratings with 2400 or 3600 lines per mm (l/mm) are only available for the UV and VIS ranges? For the NIR range, for example, there are only gratings with approx. 1100 l/mm max. available. For a working area of 3 µm, you will only get gratings with 300 l/mm. Go to even larger wavelength ranges and you will get only 150 or even 75 l/mm.
Why is that so?
Grating equation
Lithographic and holographic techniques have long helped overcome the difficulties once encountered when trying to manufacture gratings with line densities of more than 2400 l/mm (i.e. a line spacing of 420 nm). However, grating physics puts a limit to using high-resolution gratings.
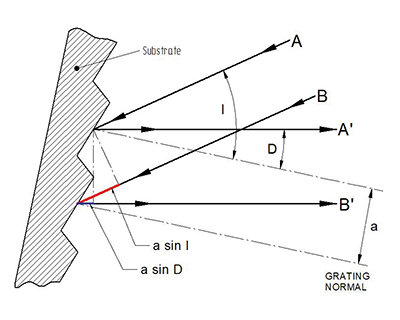
The light beams A and B of a wavelength λ incide on the adjacent lines of the grating surface. We shall call the angle of incidence relative to the grating normal I. The lines have a spacing of a.
According to the figure above the following applies to the difference in path lengths of the incident beams A and B:
DA∕B=a x sin I
Accordingly, the difference in path lengths for the diffracted beams A’ and B’ that exit the grating at a diffraction angle D relative to the grating normal is
DA‘∕B‘=a x sin D
The overall difference in path lengths for beams A’ and B’ is a difference in path lengths of
Dges=a x sin I+a x sin D
Light beams A’ and B’ interfere con-structively when the difference in path lengths is an integer multiple of the wavelength λ:
a x (sin I+sin D)=m x λ
This is the grating equation. M is the diffraction order.
Maximum wavelength of a grating
In spectrographs and monochromators, only the first diffraction order is used. All other orders are blocked with long pass filters.
For a grating with 1200 l/mm the line distance a of the lines 1/1200 mm is 833 nm. The sum of two sines cannot be greater than 2. Therefore, for m=1, the largest wavelength to fulfill the equation is:
λ= 833 nm x 2 = 1666 nm
On a grating with 2400 l/mm, the largest wavelength that can still be depicted on the exit slit in the first order is 833 nm.
However, the angles for I and D are smaller than 90° (otherwise the grating would be perpendicular to the incident light beams), so that the max-
imum wavelength that can be reached is smaller.
With a 1200 l/mm grating, monochromators can reach around 1100 nm (depending on the model).
At extreme angles in typical square gratings, the luminous intensity with the cosine of the incident angle I also changes, so that using them close to the cutoff wavelength is not useful.
To avoid this and achieve the full luminous intensity (F-number) over the entire usable wavelength range, we use for example square gratings in the size of 68 mm x 84 mm (monochromator type MSH-300).
Monochromators and spectrographs from Quantum Design
Find detailed information on gratings on our website. Please contact us for information on the versatility of our monochromators and spectrographs with focal lengths from 150 mm - 750 mm.
Contact
| +49 6157 80710-34 | |
| +49 6157 80710934 | |
| Write e-mail |